New algorithm finds the optimal bond breaking point for single molecules
Recent developments in atomic-force microscopy have enabled researchers to apply mechanical forces to individual molecules to induce chemical reactions.
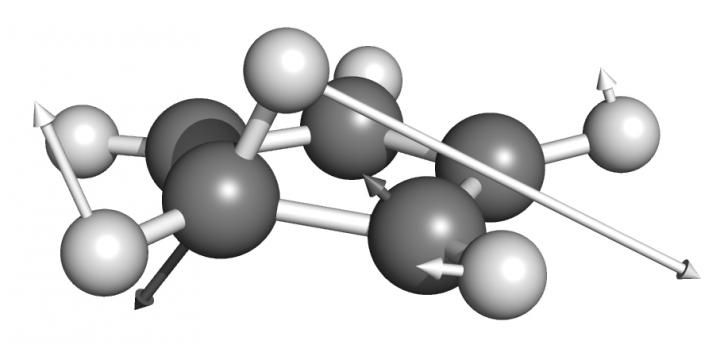
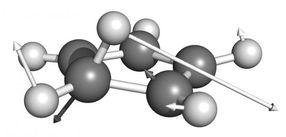
Molecular configuration of the optimal BBP of the 1, 2-sigmatropic H-shift rearrangement of cyclopentadiene. The arrows correspond to the components of the gradient at this point.
AIP Publishing
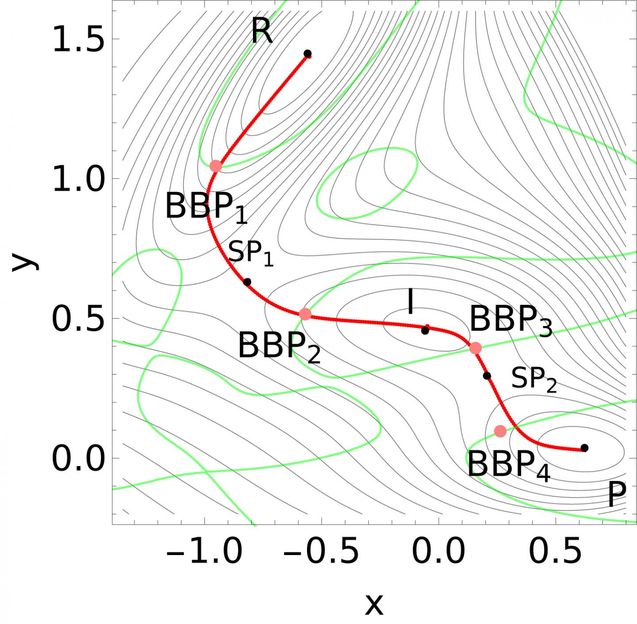
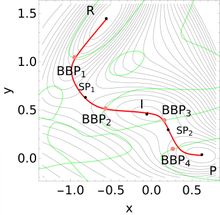
In this potential-surface picture, the red curve is a reaction pathway. The pink points are the optimal BBPs, and the black points are the minima and transition states. Green lines are the BBP points for all possible Newton trajectories.
AIP Publishing
A research team from Spain and Germany has now developed a first-of-its-kind algorithm that determines the minimal force it takes to reach the optimal bond breaking point (BBP) at the molecular level to mechanically induce a chemical reaction.
The algorithm can be applied to any molecule, including biological molecules like proteins as well as inorganic molecules. Their research has implications for numerous applications, including molecular machines, mechanically resilient and self-healing polymers, stress-responsive materials and catalyst design. The algorithm can also be used to explore how external electric fields can catalyze and control chemical reactions.
When studying mechano-chemical processes, researchers look for the mechanical response of the reactant molecule's minimum-energy structure. As the external force increases, the minimum energy and transition state structures on the force-modified potential energy surface become identical and the structure where this occurs is the sought-after BBP.
"Our work highlights that there exists another set of important points on the potential energy surface of a given system, namely the BBP, which needs to be taken into consideration for mechano-chemistry applications," said Wolfgang Quapp, a co-author of the paper who added that BBP is a new concept in mechano-chemistry.
The optimal BBPs of a potential energy surface are crucial, according to Quapp, because they provide information about the way in which tensile forces should be applied to trigger chemical transformations with the highest possible efficiency using the least amount of force.
The bond, bending and torsion of a molecule have varying stiffness. Therefore, determining the force-bearing scaffold of a molecule, to predict, for example, the point of bond rupture in an overstretched molecule, means that different directions of the external force should be tested.
"Our algorithm allows researchers to identify which part of a molecule is most susceptible to mechanical stress, and thus the algorithm is a significant step in the design of more efficient ways of harnessing mechanical energy to activate chemical reactions," Quapp said. "The importance of the optimal BBP resides in that it gives the optimal direction and magnitude of the pulling force. This necessitates an algorithm to easily find these types of points."
The algorithm is based on Newton trajectories, which come from the mathematical method of calculating zeros of a function. In the case of BBPs, the Newton trajectories are located near the reaction path of the chemical reaction under consideration.
Other news from the department science
Get the chemical industry in your inbox
From now on, don't miss a thing: Our newsletter for the chemical industry, analytics, lab technology and process engineering brings you up to date every Tuesday and Thursday. The latest industry news, product highlights and innovations - compact and easy to understand in your inbox. Researched by us so you don't have to.
