Making chaos visible
As chaos celebrates its 50th birthday, biophysicist Christian Herbst develops a new method to visualize it
Advertisement
Exactly 50 years after the US-American meteorologist Edward Lorenz discovered chaos the topic is still as fascinating as ever. A new visualization technique developed at the University of Vienna helps to make chaos visible to the naked eye. The method, which is being published in "Royal Society Interface", allows for the intuitive interpretation of chaotic or nearly chaotic phenomena, and thus makes the fascinating world of chaos theory more accessible to the scientific community.
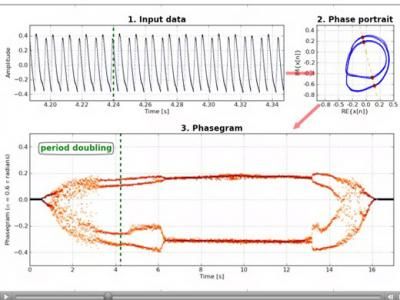
The phase space intersections are then plotted onto a graph at equally spaced time intervals (Fig. 3). The resulting phasegram is quite easy to interpret: Time is on the (horizontal) x-axis. The number and stability of lines perpendicular to the (vertical) y-axis indicates the system state at a particular point in time: one line: no oscillation (stasis) two lines: periodic oscillation four, six, eight etc. lines: period doubling, subharmonic vibrations no continuous lines, rugged appearance: irregular system behavior, indicator for chaos
Christian Herbst
The vibratory states of a dynamical (chaotic) system could to date only be visualized with methods requiring several graphs that are hard to interpret for non-mathematicians. Now a working group led by biophysicist Christian Herbst from the Department of Cognitive Biology, University of Vienna, has developed a new method for documenting chaotic phenomena: the phasegram. This novel approach, created in collaboration with chaos expert Hanspeter Herzel from the Charité in Berlin, Germany, can visualize symptoms of systems "on the way to chaos" in a single graph.
Phasegrams in a nutshel
Chaos is never pure chance or randomness. Rather, it is created by simple systems that can, under certain circumstances, generate complex irregular behaviour. This may be observed in many natural phenomena: weather, cardiac rhythm, models for population growth, economic data, some chemical reactions, or the voice of humans and animals. The long-term predictability of such systems is difficult if boundary conditions change or cannot be precisely determined in the first place – just consider the weather forecast! A periodically vibrating system can – if certain conditions are met – abruptly jump into a chaotic mode if a single system parameter undergoes only a minute change. The system could also exhibit various symptoms "on the way to chaos": so called period doubling and subharmonic oscillations. A baby's cry or the "voice crack" of a boy in puberty are lively examples of such phenomena. Voice is in general a very impressive and true-to-live example of a simple dynamical system that is capable of producing chaos. Owing to this, the phasegram method will be further exemplified with a sound sample produced by a deer larynx in the lab.
Time series data
The phasegram shown in the accompanying video was created based on a series of measurements taken at equally spaced time intervals of ca. 0.02 ms, representing the vibration of the vocal folds within the larynx. From this data, the phasegram is generated in two processing steps, which are described in more detail below: one of these is quite complex, and the other simplifies matters greatly, expressing the behaviour of the analyzed system in very simple and intuitive terms.
Phase space
Portions of the analyzed measurement data are embedded in a so-called two-dimensional phase space at equally spaced time intervals, using a mathematical method that has been described 30 years ago. The result is a geometrical figure that has distinct features which are dependent on the behaviour of the analyzed dynamical system. A cut through the phase space (see the orange diagonal line) in results in the intersections shown as red dots.
Phasegram
The phase space intersections are then plotted onto a graph at equally spaced time intervals. The resulting phasegram is quite easy to interpret: time is on the (horizontal) x-axis. The number and stability of lines perpendicular to the (vertical) y-axis indicates the system state at a particular point in time:
- one line: no oscillation (stasis)
- two lines: periodic oscillation
- four, six, eight etc. lines: period doubling, subharmonic vibration
- no continuous lines, rugged appearance: irregular system behaviour, indicator for chaos
The phasegram shows a lab-induced vocalization from a sika deer larynx. The air pressure needed to drive the vocal folds was gradually increased during the first part of the experiment (0 – 9 seconds) and gradually decreased in the second part. The experiment shows the impressive ability of a simple system to exhibit complex behavior in the form of chaos and nearly chaotic phenomena: Despite the gradual changes of air pressure the transitions between the different vibratory phenomena are abrupt. The order of the occurring vibratory modes (stasis, periodic, irregular, period doubling, periodic) is reversed in time for increasing and decreasing air pressure. The occurrence of the vibratory modes, dependent on air pressure, can be reliably reproduced in the experimental setup if boundary changes are kept stable.