Donuts and laser beams
In materials research, considerable progress is made by exploiting insights from the field of topology: Similar tools can now be applied to lasers
A donut is not a bun. From a mathematical point of view, they are two fundamentally different objects: The donut has a hole, the bun does not. A circle inside the donut around its hole in the center cannot be shrunk to a point. An arbitrary circle inside the bun, however, can.
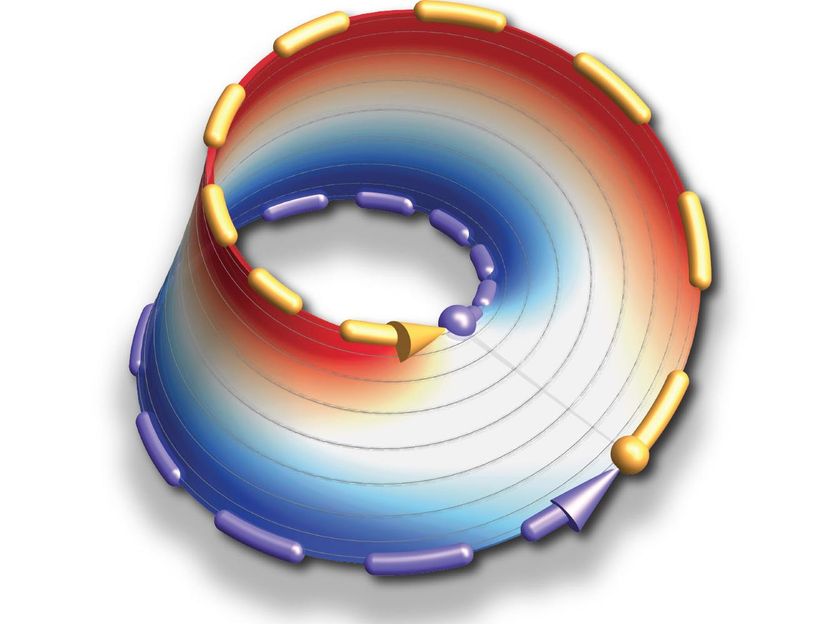
A Möbius band is a topologically non-trivial loop: If the allowed energies of the laser light follow this loop, they do not return to their initial values after one round
TU Wien

The light can travel back and forth in the two closely spaced waveguides (red and blue) and is partially reflected at their ends. The left waveguide (red) is externally pumped with energy from above. As a result of the non-trivial topological structure through which the laser light has to pass, exactly opposite interference patterns emerge at the two ends of the laser.
TU Wien


The mathematical discipline that deals with such categorizations of surfaces and bodies is topology. In recent years, its role in physics has also increased: in 2016, the Nobel Prize was awarded for the application of topological concepts to solid-state physics. Now it turns out: topology can also play a crucial role in the generation of laser light. A collaboration between the Technical University of Vienna (TU Wien) and research teams from the USA has led to the development of a special laser that emits light beams with characteristic topological properties. This success has now been published in the journal "Science".
Stable against perturbations
Topological properties are particularly interesting, among other things, because they are relatively stable against perturbations: If certain physical properties are derived only from the fact that a donut has exactly one hole, then details such as the outer circumference suddenly no longer play a role. Even a somewhat squashed donut simply does not look like a bun.
In physics, of course, not only the geometric shape of an object matters, but also its internal properties – there too, one encounters topologically interesting phenomena, albeit in a somewhat more abstract way: "The allowed energy values of a system are usually only located on certain surfaces. The topological structure of these surfaces may then determine the properties of the entire object," explains Prof. Stefan Rotter from the Institute of Theoretical Physics at TU Wien. "These are not surfaces in the three-dimensional space as we know it, but in the space of energy values – however, the principle remains the same," explains Alexander Schumer, the first author of the just-published paper. These surfaces in abstract, mathematically defined parameter spaces are also merely deformed by small perturbations, but retain their topological properties.
Theory and experiment in close collaboration
Alexander Schumer and Stefan Rotter have been investigating the topological properties of light waves with the help of computer simulations in Vienna for quite some time. How to apply the acquired knowledge to laser physics was the subject of Alexander Schumer's doctoral thesis. As part of an EU-funded project, he spent several months in California and Florida, where the research results were implemented in experiments together with the research groups there. The laser that has now been realized consists of two closely spaced waveguides (see figure). The light can propagate along these waveguides and is reflected at their ends. As it travels back and forth, the light may jump from one light waveguide to the other, and it may be amplified or attenuated by energy supplied from the outside.
"In this way, we managed to build a laser whose energies follow a topologically non-trivial loop," says Alexander Schumer. Looking at it in the ordinary three-dimensional space, the light simply travels back and forth. If, on the other hand, one charts the path taken by the light in the laser in the space of possible energy values, it turns out that the energy follows a loop around a so-called "exceptional point" – this point fulfills the function of the donut hole, so to speak, but in energy space.
"This topological loop in energy space may seem abstract and trivial, but it has a crucial implication for the light in the laser: it does not return back to its starting point when it encircles the exceptional point – similar to a trajectory on a Möbius strip," explains Alexander Schumer.
If both sides of the laser are now allowed to shine, precisely these two different end points of the path around the exceptional point in energy space become visible: the two light beams emitted by the laser in opposite directions exhibit the characteristic difference of being amplified in the center on one side and being extinguished in the center on the other side. "This is a direct consequence of the topological properties," Alexander Schumer points out.
"We have thus shown how these topological concepts are also accessible in laser physics without resorting to photonic lattices or crystal structures," says Stefan Rotter. "This could lead to important new applications, similar to the field of solid-state physics. It could potentially be used to build particularly robust, strong lasers in which you can amplify light over a long path."


























































