Laser flashes for polarized electron and positron beams
Simulations show new methods for efficient polarization: Physicists from the Max Planck Institute for Nuclear Physics in Heidelberg proposed novel methods for generation of relativistic spin polarized electron and positron beams. Using extensive simulations, they found three different scenarios for efficient polarization transfer from intense laser beams to particle beams with a high degree of polarization of up to 70%. A key mechanism is the spin-dependent radiation reaction.
Fig. 1: Scheme for spin separation of a relativistic electron beam with an elliptically polarized laser pulse.
MPIK
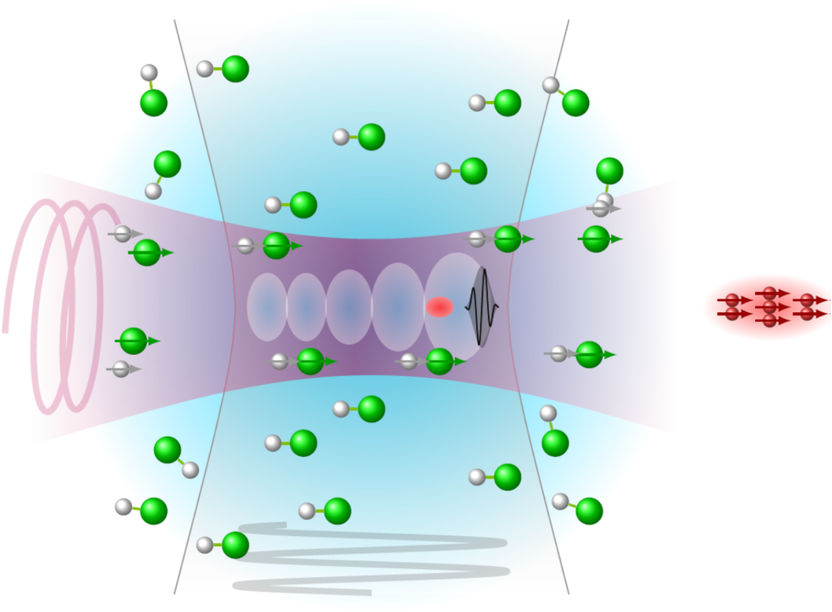
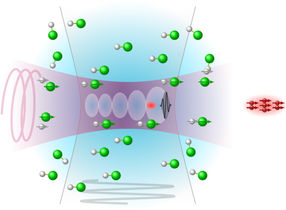
Fig. 2: Scheme of polarization-conserving laser acceleration of electrons (red) arising from a dense polarized molecular gas target (white/green). The arrows indicate the electron spin direction.
MPIK
The polarization of waves describes their direction of oscillation, for light as an electromagnetic wave this is the direction of the electric field vector. Particle beams are termed polarized if their particles have an internal angular momentum, the so-called spin, which can be imagined as a microscopic gyroscope. The polarization here describes the direction of the rotation axis. In many cases, the reciprocal interaction of light and particles depends on the polarization. In chemistry, for example, it is known that the polarization plane of light passing through a sugar solution rotates. In nuclear physics, the forces between the nucleons in an atomic nucleus are dependent on their spin. Intense polarized beams are therefore of great interest for experiments.
However, for charged particles with spin, e.g. electrons, it is very difficult to prepare the desired spin orientation. These behave like small magnetic needles and could be separated in populations with desired spin orientation by employing magnetic fields. At the same time, however, the so-called Lorentz force acts on the motion of the electrons. In order to control both influences simultaneously, location and velocity must be known very precisely - and this is fundamentally opposed by the uncertainty relation of quantum physics. Various methods have been developed to circumvent this problem, e.g. by the generation of electron beams with the preferred spin direction, or by exploiting relativistic effects in storage rings. However, these are not particularly efficient with regard to the achievable degree of polarization or the yield of polarized particles.
Physicists from Christoph Keitel's theory division at the Max Planck Institute for Nuclear Physics in Heidelberg and the Xi'ann-Jiaotong University in China around Jian-Xing Li have now proposed a new method for separating relativistic unpolarized electron beams into partial beams with opposite spin by interaction with intense polarized laser pulses [1]. For this purpose, they performed Monte Carlo simulations in which a bunch of relativistic electrons collides with a counterpropagating polarized high-intensity laser pulse. They showed that for slightly elliptically polarized light the electron beam splits into two components with opposite spin ±S (blue/red) in the direction of the smaller axis of the polarization ellipse (see Fig. 1).
This behaviour is based on the so-called radiation reaction effect. The electrons are driven back and forth in the laser field by its electrical and magnetic force, and this movement in turn leads to the emission of light quanta, which also depends on the direction of the spin. Here, the electron experiences a small recoil, which changes its direction of movement. However, for purely linear (a) or circular (b) polarization of the laser pulse, this happens in the same way for all possible directions of the oscillating fields, so that eventually electrons of the defined spin direction experiences the same deflection both to the left and to the right. For slightly elliptical polarization, however, this symmetry is broken resulting in the desired spin separation. The calculations showed up to 70% electron beam polarization.
In another study, the Heidelberg physicists investigated a process for the production of polarized positrons (antiparticles of the electron) [2]. The relativistic electrons collide with an asymmetrically linearly polarized laser pulse, the field of which is much stronger in one direction. This can be achieved by superimposing two laser pulses of different colors. By interaction of the high-energy electrons with the high-intensity laser field, electron-positron pairs are generated which are polarized in the direction of or against the magnetic component of the laser. This pair generation is a nonlinear process, which is strongly suppressed by the weaker component of the asymmetric laser field. Thus, the asymmetry of the laser pulse causes up to 60% polarization of the generated positrons which meets the requirements for applications in high energy physics.
Finally, a third paper of the Heidelberg theory Ggroup considered the generation of high-intensity polarized electron beams [3]. Recently, it has been shown experimentally that circularly polarized laser beams can be employed to generate dense electronically polarized gas targets from molecules. If such a target is illuminated with a high-intensity laser pulse, a plasma is formed in which disturbances propagate similarly to a wave, and electrons are accelerated to high energies in the "wake" of the insense laser pulse ("wakefield acceleration", see Fig. 2). One problem is the magnetic field generated in the wake, which changes the electron spin direction and can lead to beam depolarization. This magnetic field disappears exactly on the electron beam propagation axis. Using particle-in-cell simulations, the Heidelberg theorists were able to find conditions under which the accelerated electrons are strongly bunched along the beam axis. These findings pave the way to the generation of polarized electron currents in the kiloampere range, and at the same time allow to limit the depolarization to around 10%.
Original publication
[1] "Ultrarelativistic Electron-Beam Polarization in Single-Shot Interaction with an Ultraintense Laser Pulse"; Yan-Fei Li, Rashid Shaisultanov, Karen Z. Hatsagortsyan, Feng Wan, Christoph H. Keitel and Jian-Xing Li; Physical Review Letters 122, 154801 (2019).
[2] "Polarized positron beams via intense two-color laser pulses"; Yue-Yue Chen, Pei-Lun He, Rashid Shaisultanov, Karen Z. Hatsagortsyan and Christoph H. Keitel; arXiv:1904.04110.
[3] "Polarized Laser-WakeField-Accelerated Kiloampere Electron Beams"; Meng Wen, Matteo Tamburini and Christoph H. Keitel; Physical Review Letters 122, 214801 (2019).
Other news from the department science
Get the chemical industry in your inbox
From now on, don't miss a thing: Our newsletter for the chemical industry, analytics, lab technology and process engineering brings you up to date every Tuesday and Thursday. The latest industry news, product highlights and innovations - compact and easy to understand in your inbox. Researched by us so you don't have to.
